Hajítások

Vízszintes hajítás

Vízszinte hajításnál a test kezdősebessége vízszintes. A test emiatt vízszintesen egyenes vonalú egyenletes mozgást végez, másrészt egyenes vonalú egyenletesen változó mozgással esik lefelé. A két mozgás eredményeként a test egy függőleges síkban fekvő parabolapályán mozog. A parabola tengelypontja (csúcspontja) a test indulási helyénél van, a parabola tengelye függőleges.

A vízszintes hajítás kinematikai jellemzői

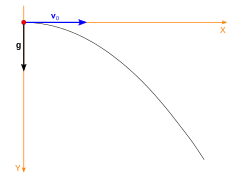
A kezdősebesség vízszintes hajításnál

A mozgás leírásához vegyünk fel egy koordinátarendszert úgy, hogy az origó a test kiindulási (t = 0-hoz tartozó) helyzeténél legyen, az Y-tengely függőlegesen lefelé mutasson, az X tengely iránya pedig egyezzen meg a v₀ kezdősebesség irányával! A mozgás kezdősebessége és a g nehézségi gyorsulás is az XY síkban helyezkedik el, így a test végig ebben a síkban mozog, azaz a Z koordináta folyamatosan nulla marad. (Emiatt a Z koordinátával a továbbiakban nem foglalkozunk.)

Gyorsulás

Mivel a test vízszintesen nem gyorsul, a g nehézségi gyorsulás pedig függőlegesen lefelé mutat, ezért a gyorsulás X, illetve Y koordinátája:

a_x = 0

a_y = -g

Sebesség

A test vízszintesen állandó v₀ sebességgel mozog, függőlegesen pedig g gyorsulással szabadon esik. Ezek alapján a X, illetve Y koordinátája:

v_x = v_0 \qquad \qquad \qquad \qquad \qquad \ \ \, \,(1)

v_y = g \cdot t \qquad \qquad \qquad \qquad \qquad \ (2)

A két összetevőből a alapján meghatározható a test sebességének nagysága:

v=\sqrt{v_x^2 + v_y^2 \ }

Elmozdulás

Az elmozdulás és összetevői

Az egyenes vonalú egyenletes mozgásra, illetve a szabadesésre vonatkozó összefüggésekből meghatározható az elmozdulás X, illetve Y koordinátája:

x=v_0 \cdot t \qquad \qquad \qquad \qquad \qquad \ (3)

y= {g \over 2} \cdot {t^2} \qquad \qquad \qquad \qquad \qquad \, (4)

A Pitagorasz-tétel alapján a két összetevőből meghatározható a test elmozdulásának nagysága:

\Delta r=\sqrt{x^2 + y^2 \ }