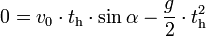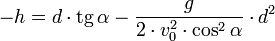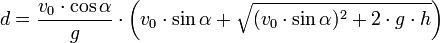Hajítások

Ferde hajítás

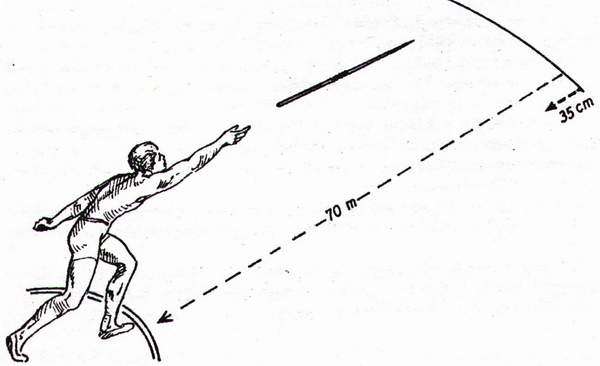
Ferde hajítás akkor jön létre, ha a test kezdősebessége nem vízszintes és nem is függőleges. A ferde hajítás két mozgás összegének tekinthető: a test vízszintesen egyenes vonalú egyenletes mozgást végez, a mozgás függőlegesösszetevője pedig egyenes vonalú egyenletesen változó mozgás.

Ferde hajítás felfelé

Ha 0° < α < 90°, akkor a test először emelkedik, majd a maximális magasság elérése után mindaddig süllyed, amíg el nem éri a talajt (vagy bele nem ütközik valamibe). Ha a talaj nem vízszintes, akkor előfordulhat, hogy a test a kiindulási szint alá kerül, azaz az Y koordinátája negatívvá válik.

A ferde hajítás távolsága

Ha a test a vízszintes talajról indul, akkor a hajítás távolsága az a d távolság, amelyet a test vízszintesen megtesz addig, amíg újra visszaér a kiindulási szintre (y = 0). Ha az ehhez szükséges időtartamot t_h jelöli, akkor a (4) alapján:

0=v_0 \cdot t_{\mathrm{h}} \cdot \sin\alpha - {g \over 2} \cdot {t_{\mathrm{h}}^2}

Ebből a hajítás időtartama:

t_{\mathrm{h}} = {2 \cdot v_0 \cdot \sin\alpha \over g}

Ezt a (3) egyenletbe helyettesítve, továbbá egy trigonometrikus azonosságot felhasználva igazolható, hogy a hajítás távolsága:

d= {v_0^2 \cdot \sin (2\cdot\alpha) \over g}

Adott v₀ és g esetén a hajítás távolsága az α szögtől függ. A távolság akkor lesz a legnagyobb, ha a képletben a szinuszfüggvény a maximális értéket (=1) veszi fel. Ez akkor következik be, ha az α szög 45°. Adott kezdősebesség és nehézségi gyorsulás mellett tehát a hajítás távolsága 45°-os kezdősebességnél a legnagyobb.

A ferde hajítás magassága

A hajítás magassága a kiindulási szint és a pálya tetőpontja közti h szintkülönbség. A test emelkedése addig tart, amíg a sebesség függőleges összetevője 0 nem lesz. Ha az emelkedés időtartamát t_e jelöli, akkor a (2) alapján:

0=v_0 \cdot \sin\alpha - g \cdot t_{\mathrm{e}}

Ebből az emelkedés időtartama:

t_{\mathrm{e}} = {v_0 \cdot \sin\alpha \over g}

Ezt az (4) egyenletbe helyettesítve a hajítás magassága:

h = {v_0^2 \cdot \sin^2\alpha \over {2 \cdot g}}

Ferde hajítás lefelé

A ferde hajítás távolsága lefelé történő hajításnál

Ha -90° < α < 0°, akkor a test mindaddig süllyed, amíg el nem éri a talajt (vagy bele nem ütközik valamibe). Emiatt a test folyamatosan a kiindulási szint alatt halad, azaz az Y koordinátája negatív.

Ha a test a vízszintes talaj feletti pontból indul, akkor a hajítás távolsága az a d távolság, amelyet a test vízszintesen megtesz a talajra érkezésig. Ha az indulási hely h magasságban van a talaj felett, akkor a talajra érkezéskor y = –h, így az (5) alapján:

-h=d \cdot \mbox{tg}\, \alpha - {g \over {2 \cdot {v_0^2 \cdot \cos^2\alpha}}} \cdot d^2

Ennek a másodfokú egyenletnek egyetlen pozitív megoldása van:

d = \frac{v_0 \cdot \cos\alpha}{g} \cdot \left( v_0 \cdot \sin\alpha + \sqrt{(v_0 \cdot \sin\alpha )^2 + 2 \cdot g \cdot h} \right)

Megjegyzés: Az előző gondolatmenetben az α szögre semmiféle feltétel sem szerepel, ezért a hajítás d távolságára kapott fenti összefüggés afelfelé történő ferde hajításra, sőt a vízszintes hajításra is érvényes.